När man studerar fördelningen av inkomster och förmögenheter med mått som Gini-koefficienten eller Theil-koefficienten är det vanligt att man bryter ner fördelningen på skillnader mellan grupper och skillnader inom grupper. Om vi studerar inkomstfördelningen i Sverige idag skulle man t ex kunna bryta ner Gini-koefficienten för inkomster på hur mycket som beror på den genomsnittliga inkomstskillnaden mellan män och kvinnor, och hur mycket som beror på skillnaden inom gruppen män och inom gruppen kvinnor. Detta är mellan-komponenten och inom-komponenten. Ett annat exempel kommer från en artikel som Anna Missiaia, Mats Olsson och jag publicerade 2018, om fördelningen av förmögenheter i Sverige 1750 till 1900. I tabellen nedan visar vi Gini-koefficienten totalt samt för fyra olika sociala grupper: adeln, borgerligheten, bönderna, och en bred grupp "arbetare och lägre medelklass". Vi ser t ex att Gini-koefficienten totalt år 1750 var 0.79 men att den inom gruppen bönder bara var 0.57. Av någon anledning har vi sedan när vi ska bryta ner den totala ojämlikheten på mellan- och inom-komponenter, gått över till Theil, vilket är det som syns längst ner. Där ser vi att inom-komponenten är den större delen av Theil varje år. Vad betyder då det?
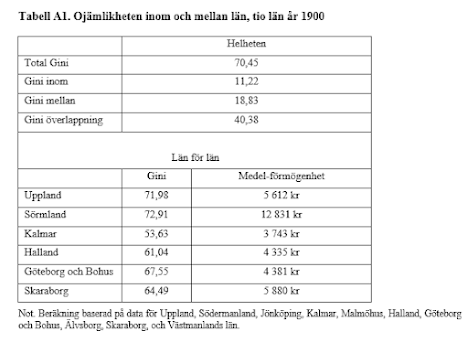
"Contrary to his detailed and deductive analysis of the changes in the between and within components, Milanovic relies on intuition along with some simulations to interpret overlap behaviour, and remarks that "every synthetic index of inequality, and the Gini is no exception to that, is a very complex statistic" (page 80). Needless to say, then, there is plenty of room - and need - for some more analytical underpinning of the behaviour of the Gini overlap term. That is the purpose of our paper." (s. 2)Jag är själv i en situation där jag har en Gini-koefficient med en stor överlappningskomponent som jag vill tolka. Jag har samlat in förmögenhetstaxeringen för 8053 skattebetalare i tio svenska län år 1900. Fördelningen per län ser ut så här:
Av en Gini på 70,5 står alltså överlappningen för 40,4 punkter. Därför blir det intressant att tolka inte bara inom- och mellan-komponenterna, utan också överlappningen.
Lambert och Decoster menar att Gini-dekompositionerna började med Bhattacharya och Mahalanobis (1967) och fortsatte med Pyatt (1976) och Mookherjee och Shorrocks (1982). De senare menade att överlappnings-residualen var en "awkward interaction effect... impossible to interpret with any precision, except to say that it is the residual necessary to maintain the identity". Sedan 1980-talet har forskare också tagit fram "decomposable" ojämlikhets-index som inte skapar någon sådan besvärlig residual: bland dessa studier finns Bourguignon (1979), Shorrocks (1980) och Cowell (1980).
I sin egen analys börjar Lambert och Decoster med två sub-grupper, a och b, som kan beteckna regioner eller någon annan socioekonomisk uppdelning av befolkningen.
"Milanovic (2002), in contrast, seems comfortable with the overlap contribution to the Gini decomposition, describing it in the context of world inequality analysis as measuring the degree of homogeneity within regions: “the more important the overlapping component... the less one’s income depends on where she lives”. Milanovic also attributes an increase in world overlap over time to the changing situations in India and China, occurring as “more people from these poor countries ‘mingle’ with people from rich countries”" (cit. s. 6)
Referens
Peter J Lambert och André Decoster (2005) "The Gini coefficient reveals more", center for Economic Studies Dsicussion Paper Series 05.08, KU Leuven.



Inga kommentarer:
Skicka en kommentar